Problem:
For a set of four distinct lines in a plane, there are exactly distinct points that lie on two or more of the lines. What is the sum of all possible values of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
There are several cases to consider.
If all four lines are concurrent, then there is intersection point.
If three of the lines are concurrent and the fourth line is parallel to one of those three, then there are intersection points. If three of the lines are concurrent and the fourth line is parallel to none of those three, then there are intersection points.
In the remaining cases no three lines are concurrent. If they are all parallel, then there are intersection points.
If only three of them are parallel, then there are again intersection points.
If two of them are parallel but no three are mutually parallel, then there are either again intersection points, if the other two lines are parallel to each other; or intersection points, if the other two lines intersect.
In the final case, every line intersects every other line, giving points of intersection.
These are all the cases, so the requested sum is .
The problem deals with the possible number of intersection points when four distinct lines are drawn in the plane. The maximum number of intersection points is . The diagram shows that the number of intersection points can be , and .
.jpg)
0
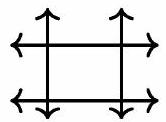
4
.jpg)
1
.jpg)
5
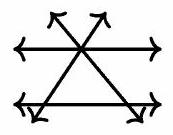
3
.jpg)
6
To see that there cannot be points of intersection, suppose to the contrary that and are the only points of intersection among the four lines. If and lie on one of the lines, then the other three lines, , and , must all pass through or , with at least one line passing through each. Without loss of generality, suppose contains , and and contain . At most one of and can be parallel to , and thus there will be a third intersection point. Otherwise it must be the case that is the intersection of two of the lines, and is the intersection of the other two lines; say is the intersection of and , and is the intersection of and . Again, and cannot both be parallel to , and thus there must be another point of intersection.
As in the first solution, the requested sum is .
Note: Students who wish to pursue further interesting questions about arrangements of points and lines, such as the dual problem to this one (how many lines points can determine), might want to start by looking up the Sylvester-Gallai Theorem.
The problems on this page are the property of the MAA's American Mathematics Competitions