Problem:
A paint brush is swept along both diagonals of a square to produce the symmetric painted area, as shown. Half the area of the square is painted. What is the ratio of the side length of the square to the brush width?
.jpg)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let be the side length of the square, let be the width of the brush, and let be the leg length of one of the congruent unpainted isosceles right triangles. Since the unpainted area is half the area of the square, the area of each unpainted triangle is of the area of the square. So
The leg length plus the brush width is equal to half the diagonal of the square, so . Thus
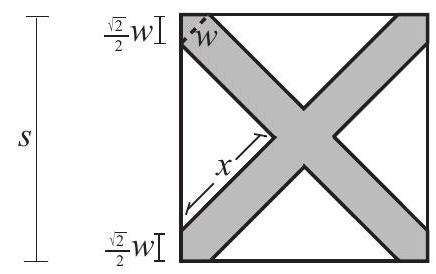
The painted stripes have isosceles right triangles with hypotenuse at each vertex of the square, and the legs of these triangles have length . Since the total area of the four congruent unpainted triangles is half the area of the original square, we have
and
The problems on this page are the property of the MAA's American Mathematics Competitions