Problem:
Two transformations are said to commute if applying the first followed by the second gives the same result as applying the second followed by the first. Consider these four transformations of the coordinate plane:
- A translation 2 units to the right,
- A 90∘-rotation counterclockwise about the origin,
- A reflection across the x-axis, and
- A dilation centered at the origin with scale factor 2 .
Of the 6 pairs of distinct transformations from this list, how many commute?
Answer Choices:
A. 1
B. 2
C. 3
D. 4
E. 5
Solution:
Denote the transformations by T,R,F, and D in the order given in the problem statement. Then the images of point (x,y) are T(x,y)=(x+2,y),R(x,y)=(−y,x),F(x,y)= (x,−y), and D(x,y)=(2x,2y). The results of applying a pair of transformations in either order are as follows:
- T(R(x,y))=T(−y,x)=(−y+2,x) and R(T(x,y))=R(x+2,y)=(−y,x+2). The results are different, so T and R do not commute.
- T(F(x,y))=T(x,−y)=(x+2,−y) and F(T(x,y))=F(x+2,y)=(x+2,−y). The results are the same, so T and F do commute.
- T(D(x,y))=T(2x,2y)=(2x+2,2y) and D(T(x,y))=D(x+2,y)=(2x+4,2y). The results are different, so T and D do not commute.
- R(F(x,y))=R(x,−y)=(y,x) and F(R(x,y))=F(−y,x)=(−y,−x). The results are different, so R and F do not commute.
- R(D(x,y))=R(2x,2y)=(−2y,2x) and D(R(x,y))=D(−y,x)=(−2y,2x). The results are the same, so R and D do commute.
- D(F(x,y))=D(x,−y)=(2x,−2y) and F(D(x,y))=F(2x,2y)=(2x,−2y). The results are the same, so D and F do commute.
Thus (C)3 of the 6 pairs commute.
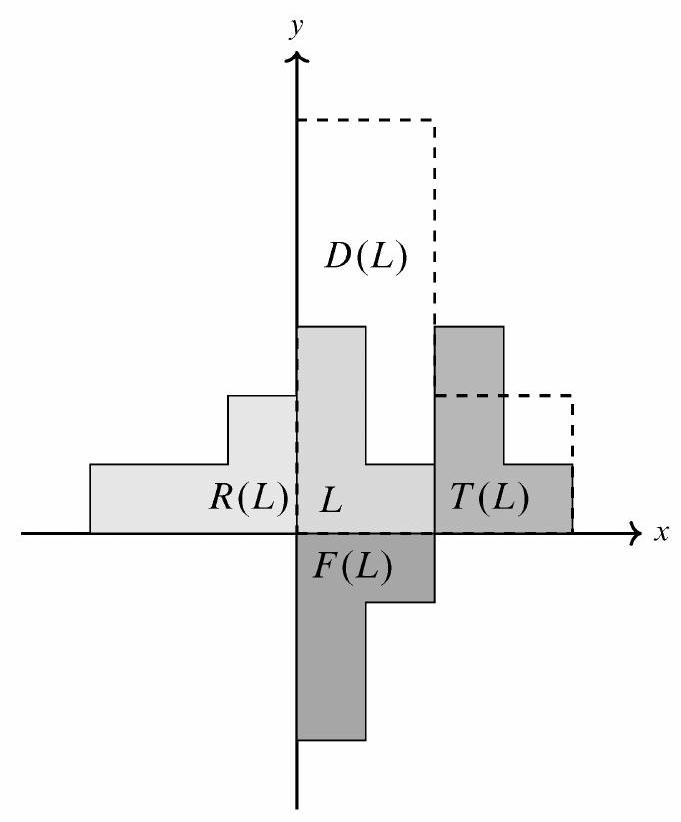
Note: The following figure illustrates the application of each transformation to an L-shaped figure.
The problems on this page are the property of the MAA's American Mathematics Competitions