Problem:
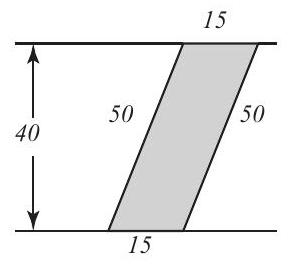
A street has parallel curbs feet apart. A crosswalk bounded by two parallel stripes crosses the street at an angle. The length of the curb between the stripes is feet and each stripe is feet long. Find the distance, in feet, between the stripes.
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The crosswalk is in the shape of a parallelogram with base feet and altitude feet, so its area is . But viewed another way, the parallelogram has base feet and altitude equal to the distance between the stripes, so this distance must be feet.
Answer: .
The problems on this page are the property of the MAA's American Mathematics Competitions