Problem:
A rectangle and a rectangle are contained within a square without overlapping at any interior point, and the sides of the square are parallel to the sides of the two given rectangles. What is the smallest possible area of the square?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The side length of the square is at least equal to the sum of the smaller dimensions of the rectangles, which is .
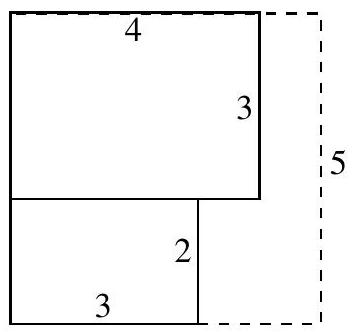
If the rectangles are placed as shown, it is in fact possible to contain them within a square of side length . Thus the smallest possible area is .
The problems on this page are the property of the MAA's American Mathematics Competitions