Problem:
A cube is constructed from white unit cubes and black unit cubes. How many different ways are there to construct the cube using these smaller cubes? (Two constructions are considered the same if one can be rotated to match the other.)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
This problem is about the relationships between the white unit cubes and the blue unit cubes, which can be solved by Graph Theory. We use a Planar Graph to represent the larger cube. Each vertex of the planar graph represents a unit cube. Each edge of the planar graph represents a shared face between neighboring unit cubes. Each face of the planar graph represents a face of the larger cube.
Now the problem becomes a Graph Coloring problem of how many ways to assign vertices blue and vertices white with Topological Equivalence. For example, in Figure , as long as the blue vertices belong to the same planar graph face, the different planar graphs are considered to be topological equivalent by rotating the larger cube.
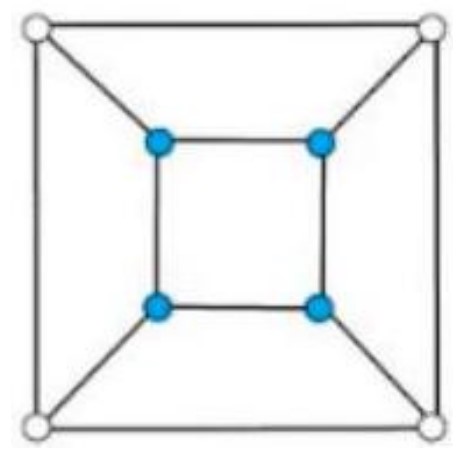
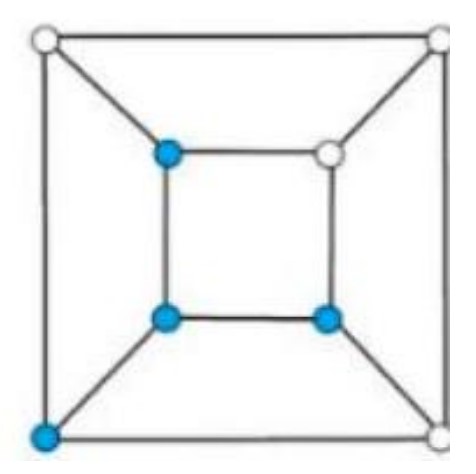
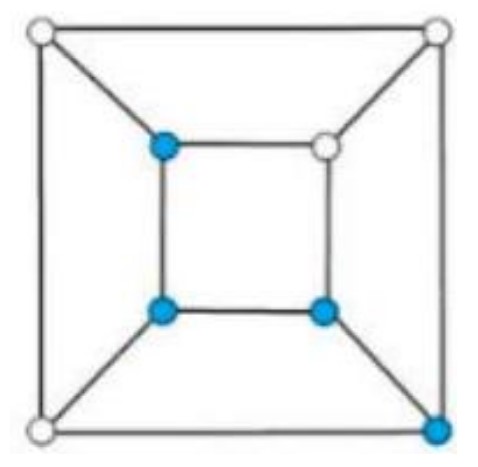
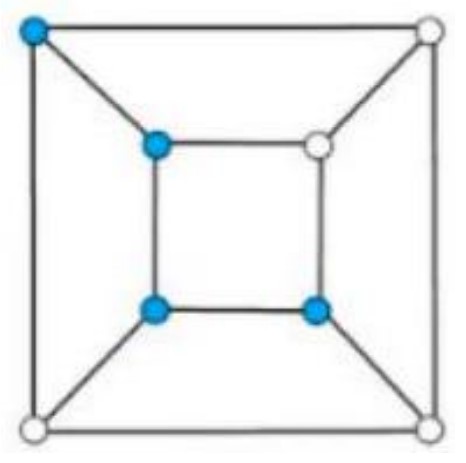
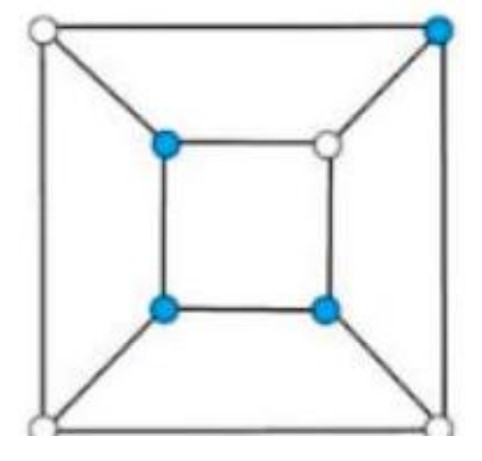
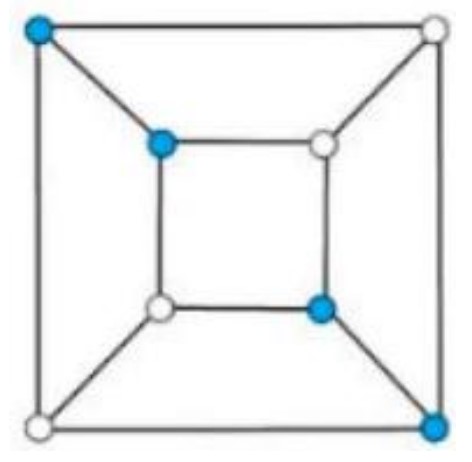
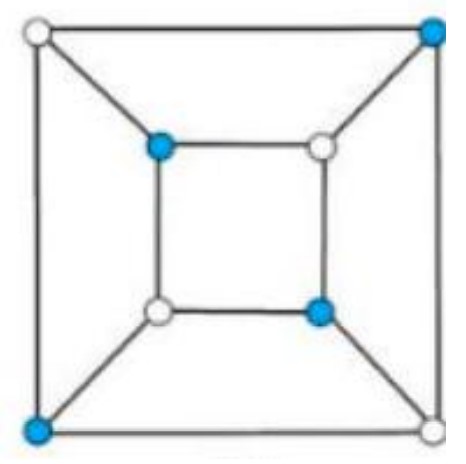
Here is how the blue unit cubes are arranged:
In Figure : blue unit cubes are on the same layer (horizontal or vertical).
In Figure : blue unit cubes are in shape.
In Figure and : blue unit cubes are in shape.
In Figure : blue unit cubes are in shape, and the other is isolated without a shared face.
In Figure : pairs of neighboring blue unit cubes are isolated from each other without a shared face.
In Figure : blue unit cubes are isolated from each other without a shared face.
So the answer is .
The problems on this page are the property of the MAA's American Mathematics Competitions