Problem:
In rectangle ABCD,AB=6 and BC=3. Point E between B and C, and point F between E and C are such that BE=EF=FC. Segments AE and AF intersect BD at P and Q, respectively. The ratio BP:PQ:QD can be written as r:s:t, where the greatest common factor of r,s, and t is $$. What is r+s+t?
Answer Choices:
A. 7
B. 9
C. 12
D. 15
E. 20
Solution:
Triangles APD and EPB are similar and BE:DA=1:3, so BP=41BD. Triangles AQD and FQB are similar and BF:DA=2:3, so BQ=52BD and QD=53BD. Then PQ=BQ−BP=(52−41)BD=203BD. Thus BP:PQ:QD=41:203:53=5:3:12, and r+s+t=5+3+12=(E)20.
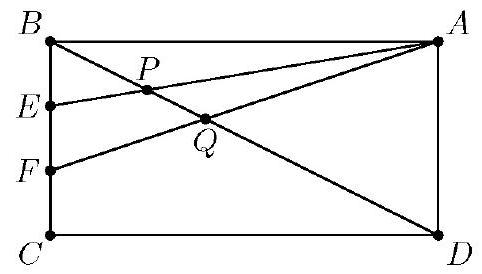
Note: The answer is independent of the dimensions of the original rectangle. Consider the figures below, showing the rectangle ABCD with points E and F trisecting side BC. Let G and H trisect AD, and let M and N be the midpoints of AB and CD. Then the segments AE,GF, and HC are equally spaced, implying that BP=PR=RS=SD and showing that BP:PD : BD=1:3:4=5:15:20. The segments ME,AF,GC, and HN are also equally spaced, implying that BT=TQ=QU=UV=VD and showing that BQ:QD:BD=2:3:5=8:12:20. It then follows that BP:PQ:QD= 5:(15−12):12=5:3:12.
.jpg)
The problems on this page are the property of the MAA's American Mathematics Competitions

.jpg)