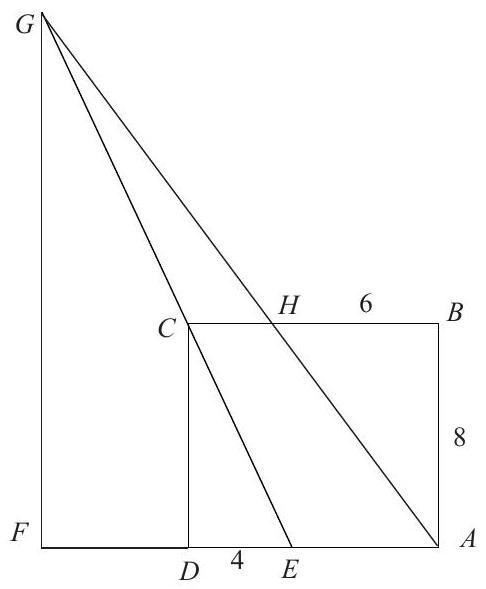
Problem:
In rectangle ABCD, we have AB=8,BC=9,H is on BC with BH=6,E is on AD with DE=4, line EC intersects line AH at G, and F is on line AD with GF⊥AF. Find the length GF.
Answer Choices:
A. 16
B. 20
C. 24
D. 28
E. 30
Solution:
We have EA=5 and CH=3. Triangles GCH and GEA are similar, so
GEGC=53 and GECE=GEGE−GC=1−53=52.
Triangles GFE and CDE are similar, so
8GF=GECE=25
and FG=20.
OR
Place the figure in the coordinate plane with the origin at D,DA on the positive x-axis, and DC on the positive y-axis. Then H=(3,8) and A=(9,0), so line AG has the equation
y=−34x+12.
Also, C=(0,8) and E=(4,0), so line EG has the equation
y=−2x+8.
The lines intersect at (−6,20), so FG=20.
Answer: B.
The problems on this page are the property of the MAA's American Mathematics Competitions