Problem:
Two straight pipes (circular cylinders), with radii 1 and , lie parallel and in contact on a flat floor. The figure below shows a head-on view. What is the sum of the possible radii of a third parallel pipe lying on the same floor and in contact with both?
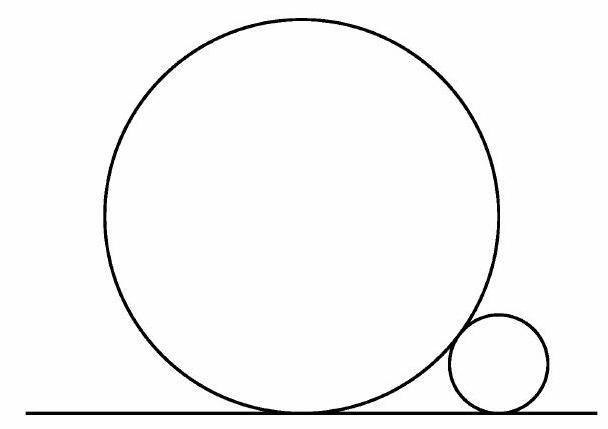
Answer Choices:
A.
B.
C.
D.
E.
Solution:
There are two possible positions for the third pipe-either nestled in the gap between the pipes or outside. See the figure below.
.jpg)
Consider the blown-up figure below. In this diagram, is the center of the circle of radius is the center of the circle of radius , and is the center of the third circle nestled in the gap. The horizontal lines through and intersect the vertical line through at and , respectively, and is the foot of the perpendicular from to .
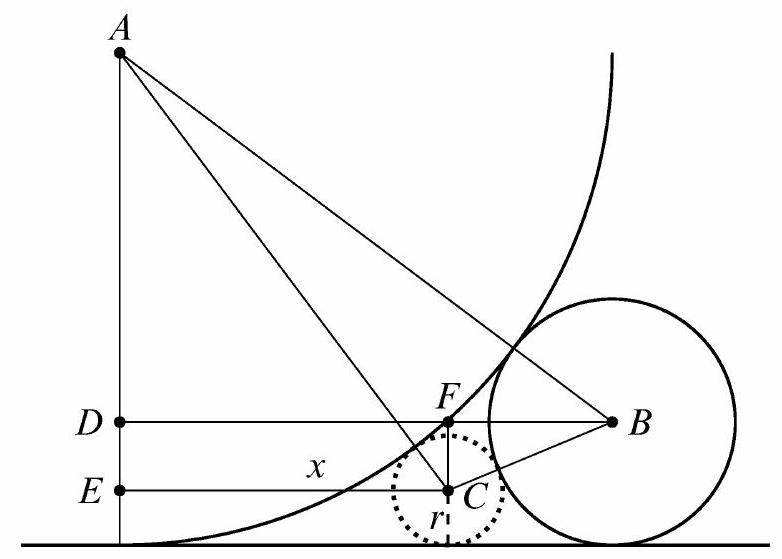
Because and , it follows that is a 3-4-5 right triangle scaled down by a factor of 4 , so . Thus the vertical line through is tangent to the given circle of radius 1 . Then by symmetry, the radius of the larger of the two dashed circles tangent to both given circles has radius 1 .
It remains to compute the radius of the smaller dashed tangent circle. Let . The Pythagorean Theorem in gives , which simplifies to . The Pythagorean Theorem in gives
which simplifies to . Combining these equations gives , which is equivalent to and . Because , the relevant solution is , and the radius of the smaller circle is .
The requested sum of possible radii is .
The problems on this page are the property of the MAA's American Mathematics Competitions