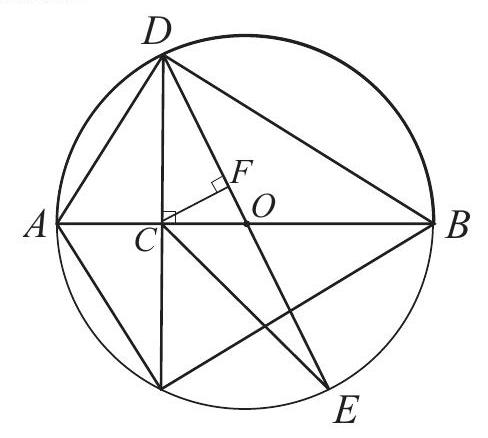
Problem:
Let AB be a diameter of a circle and C be a point on AB with 2⋅AC=BC. Let D and E be points on the circle such that DC⊥AB and DE is a second diameter. What is the ratio of the area of △DCE to the area of △ABD?
Answer Choices:
A. 61
B. 41
C. 31
D. 21
E. 32
Solution:
Let O be the center of the circle. Each of △DCE and △ABD has a diameter of the circle as a side. Thus the ratio of their areas is the ratio of the two altitudes to the diameters. These altitudes are DC and the altitude from C to DO in △DCE. Let F be the foot of this second altitude. Since △CFO is similar to △DCO,
DCCF=DOCO=DOAO−AC=21AB21AB−31AB=31
which is the desired ratio.
OR
Because AC=AB/3 and AO=AB/2, we have CO=AB/6. Triangles DCO and DAB have a common altitude to AB so the area of △DCO is 61 the area of △ADB. Triangles DCO and ECO have equal areas since they have a common base CO and their altitudes are equal. Thus the ratio of the area of △DCE to the area of △ABD is 31.
Answer: C.
The problems on this page are the property of the MAA's American Mathematics Competitions
.jpg)