Problem:
The area of the region bounded by the graph of
is , where and are integers. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The lines and divide the coordinate plane into four regions. In the region including the positive -axis, and , so
which is equivalent to
In the region including the positive -axis, and , so
which is equivalent to
Similarly, in the region including the negative -axis, the defining equation is equivalent to , and in the region including the negative -axis, the defining equation is equivalent to .
The complete graph, shown below, therefore consists of four semicircles whose diameters form a square of side length 6. The enclosed area is thus . The requested sum is .
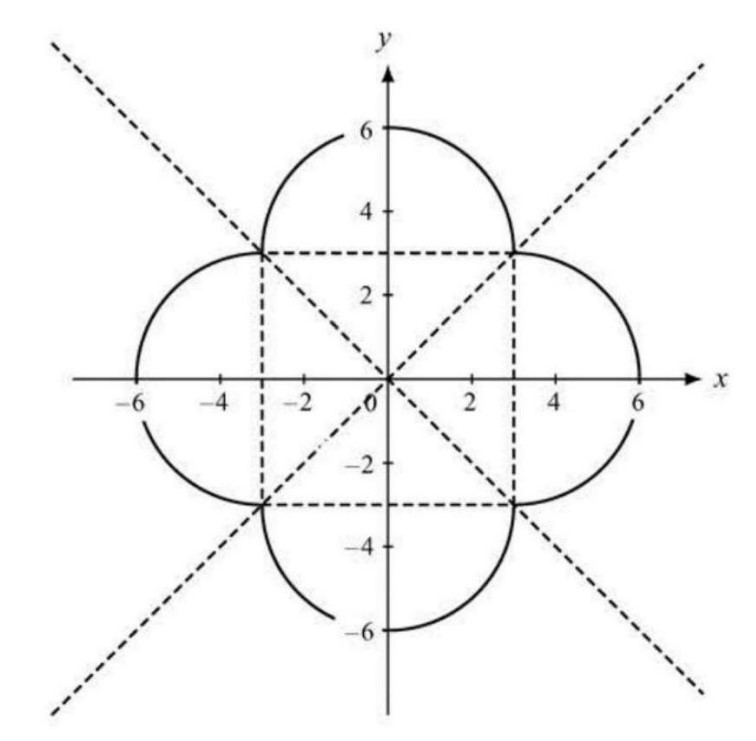
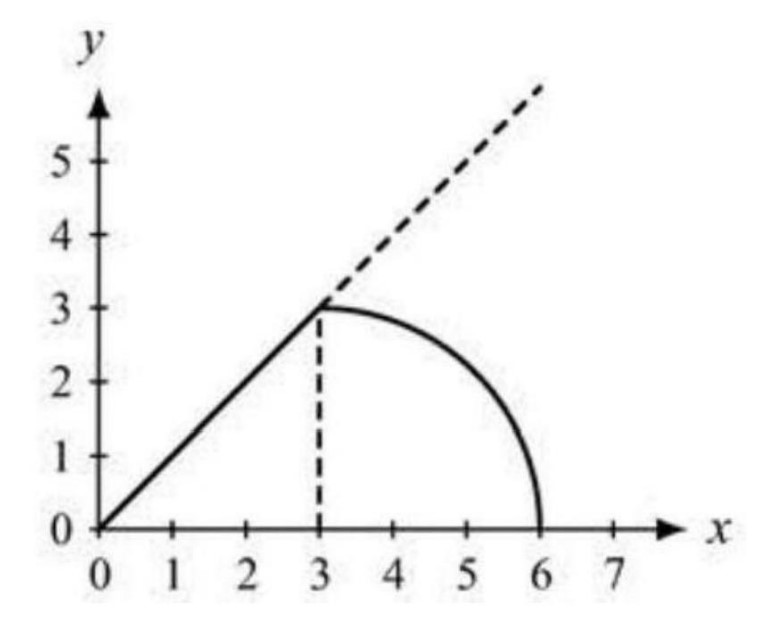
The given curve is symmetric with respect to the -axis, with respect to the -axis, with respect to the line , and with respect to the line . Hence the area in question is times the area of that part of the region that lies in the wedge , bounded by the curve . This is equivalent to and is a circle with center and radius . As seen in the figure below, this gives rise to a triangle with vertices at , and together with a quarter circle of radius centered at extending from counterclockwise to with vertices , and . The area of this region is . The total area is times this, which is , and the requested sum is .
The problems on this page are the property of the MAA's American Mathematics Competitions