Problem:
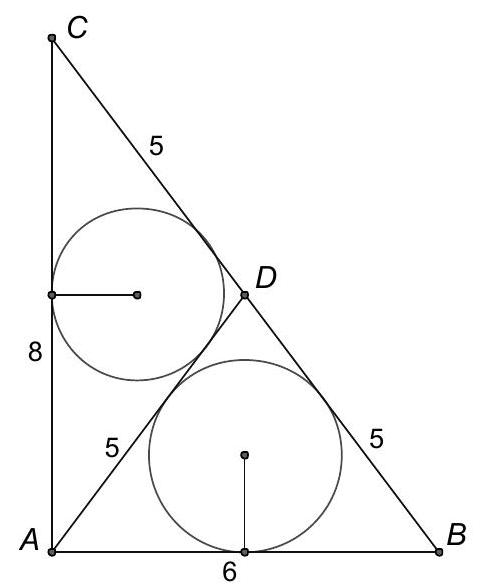
In â–³ABC,AB=6,AC=8,BC=10, and D is the midpoint of BC. What is the sum of the radii of the circles inscribed in â–³ADB and â–³ADC?
Answer Choices:
A. 5​
B. 411​
C. 22​
D. 617​
E. 3
Solution:
By the converse of the Pythagorean Theorem, ∠BAC is a right angle, so BD=CD=AD=5, and the area of each of the small triangles is 12 (half the area of △ABC). The area of △ABD is equal to its semiperimeter, 21​⋅(5+5+6)=8, multiplied by the radius of the inscribed circle, so the radius is 812​=23​. Similarly, the radius of the inscribed circle of △ACD is 34​. The requested sum is 23​+34​=(D)617​​.
