Problem:
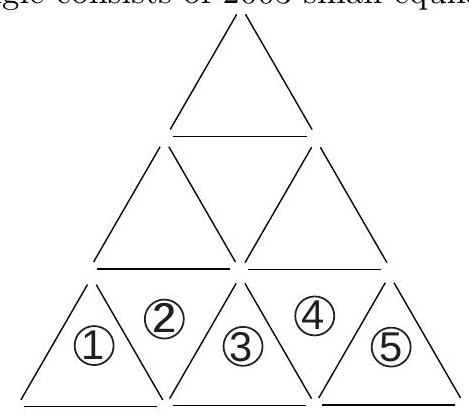
A large equilateral triangle is constructed by using toothpicks to create rows of small equilateral triangles. For example, in the figure we have 3 rows of small congruent equilateral triangles, with 5 small triangles in the base row. How many toothpicks would be needed to construct a large equilateral triangle if the base row of the triangle consists of 2003 small equilateral triangles?
Answer Choices:
A. 1,004,004
B. 1,005,006
C. 1,507,509
D. 3,015,018
E. 6,021,018
Solution:
The base row of the large equilateral triangle has 1001 triangles pointing downward and 1002 pointing upward. This base row requires 3(1002) toothpicks since the downward pointing triangles require no additional toothpicks. Each succeeding row will require one less set of 3 toothpicks, so the total number of toothpicks required is
3(1002+1001+1000+⋯+2+1)=3⋅21002⋅1003=1,507,509.
OR
Create a table:
Number of Rows123 ⋮nNumber of Trianglesin Base Row135 ⋮2n−1Number of Toothpicksin All Rows33+63+6+9 ⋮3(1+2+⋯+n)
Thus
2003=2n−1 so n=1002.
The number of toothpicks is
3(1+2+⋯+1002)=32(1002)(1003)=1,507,509.
Answer: C.
The problems on this page are the property of the MAA's American Mathematics Competitions