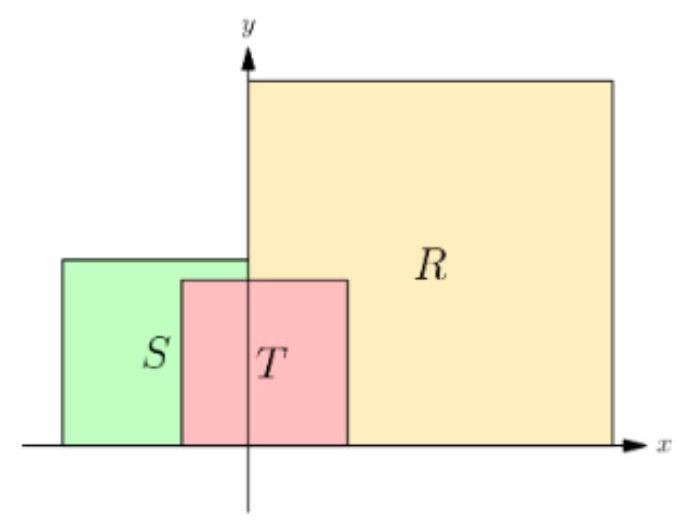
Problem:
Let , and be squares that have vertices at lattice points (i.e., points whose coordinates are both integers) in the coordinate plane, together with their interiors. The bottom edge of each square is on the -axis. The left edge of and the right edge of are on the -axis, and contains as many lattice points as does . The top two vertices of are in , and contains of the lattice points contained in . See the figure (not drawn to scale).
The fraction of lattice points in that are in is times the fraction of lattice points in that are in . What is the minimum possible value of the edge length of plus the edge length of plus the edge length of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let , and be the respective edge lengths of , and , and let , , and be the respective sets of lattice points in , and . Then there is an integer such that and , and , and . Because contains lattice points on the -axis, . Thus , so is even. Furthermore, if is a multiple of 4 , then the greatest power of 2 that divides the right side is odd, so .\
Note that
implying that . If the lower left vertex of is , then the lower right vertex is , and
Therefore , from which , and . Hence for some positive integer . The least possible value of is 50 , giving . The squares in this case have side lengths 149,99 , and 89 , and the requested sum is . (Thus it turns out that contains 22500 lattice points, contains 10000 lattice points, contains 8100 lattice points, 630 lattice points of are contained in , and 7560 lattice points of are contained in .)
The problems on this page are the property of the MAA's American Mathematics Competitions