Problem:
Real numbers between and , inclusive, are chosen in the following manner. A fair coin is flipped. If it lands heads, then it is flipped again and the chosen number is if the second flip is heads, and if the second flip is tails. On the other hand, if the first coin flip is tails, then the number is chosen uniformly at random from the closed interval . Two random numbers are chosen independently in this manner. What is the probability that ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The probability that the first coin flip for both and is heads is , and in half of these cases will be and in the other half of these cases will be . This contributes to the probability that .
The probability that the first coin flip for is heads and the first coin flip for is tails or vice versa is . In such cases, one of the variables is or , and the probability that is . This contributes to the probability that .
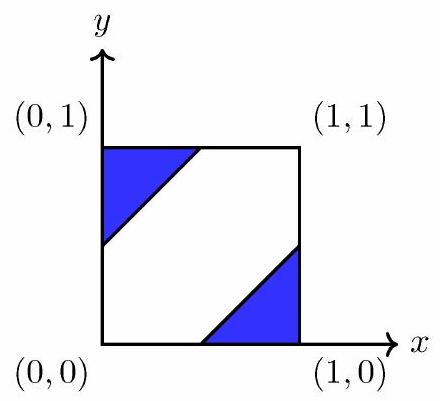
Finally, of the time both and will be chosen uniformly from . In this case, the situation can be modeled by the following diagram, in which the area of the shaded region gives the probability that . This contributes to the probability that . The requested probability is .
The problems on this page are the property of the MAA's American Mathematics Competitions