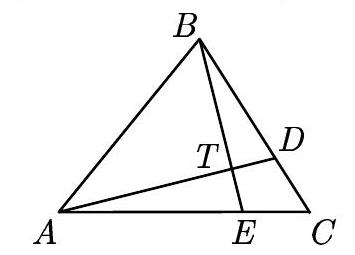
Problem:
In △ABC points D and E lie on BC and AC, respectively. If AD and BE intersect at T so that AT/DT=3 and BT/ET=4, what is CD/BD?
Answer Choices:
A. 81
B. 92
C. 103
D. 114
E. 125
Solution:
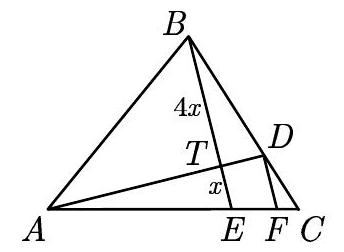
Let F be a point on AC such that DF is parallel to BE. Let BT=4x and ET=x.
Because △ATE and △ADF are similar, we have
xDF=ATAD=34, and DF=34x
Also, △BEC and △DFC are similar, so
BCCD=BEDF=5x4x/3=154
Thus
BDCD=1−(CD/BC)CD/BC=1−4/154/15=(D)114.
OR
Let s=Area(△ABC). Then
Area(△TBC)=41s and Area(△ATC)=51s
so
Area(△ATB)=Area(△ABC)−Area(△TBC)−Area(△ATC)=2011s
Hence
BDCD=Area(△ABD)Area(△ADC)=Area(△ATB)Area(△ATC)=11s/20s/5=114
Answer: D.
The problems on this page are the property of the MAA's American Mathematics Competitions