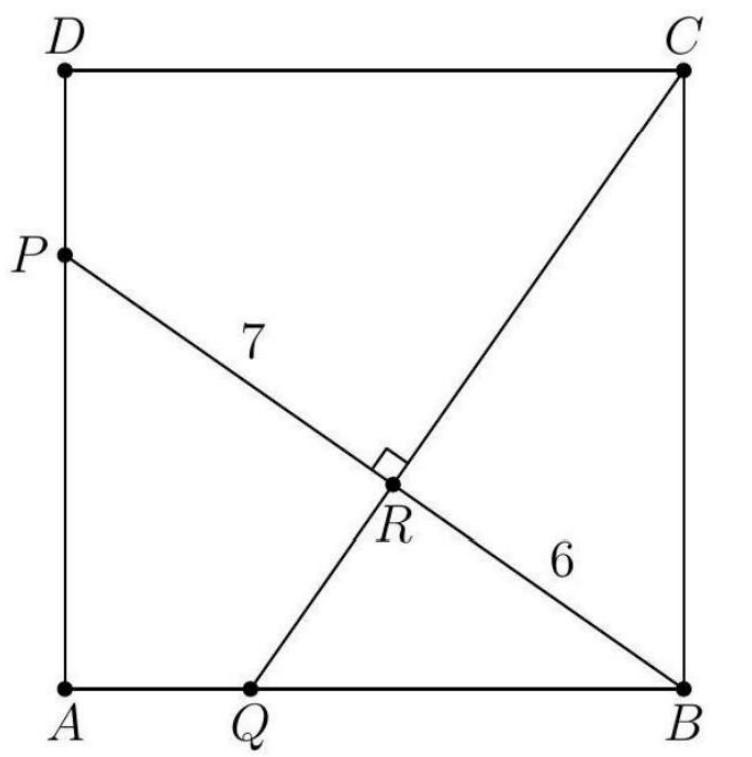
Problem:
In square , points and lie on and , respectively. Segments and intersect at right angles at , with and . What is the area of the square?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Note that . Then, it follows that . Thus, . Define to be the length of side , then . Because is the altitude of the triangle, we can use the property that: . Substituting the given lengths, we have:
Solving gives and . We eliminate the possibility of because . Thus, the side length of the square, by the Pythagorean Theorem, is:
Thus, the area of the square is: . So, the answer is .
Note There is another way to prove that is impossible. If , then the side length would be and the area would be , but that isn’t in the answer choices. Thus, must be .
The problems on this page are the property of the MAA's American Mathematics Competitions