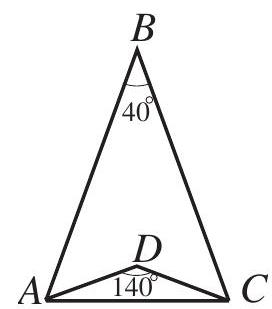
Problem:
Triangles ABC and ADC are isosceles with AB=BC and AD=DC. Point D is inside △ABC,∠ABC=40∘, and ∠ADC=140∘. What is the degree measure of ∠BAD?
Answer Choices:
A. 20
B. 30
C. 40
D. 50
E. 60
Solution:
Because △ABC is isosceles, ∠BAC=21(180∘−∠ABC)=70∘.
Similarly,
∠DAC=21(180∘−∠ADC)=20∘.
Thus ∠BAD=∠BAC−∠DAC=(D)50∘.
OR
Because △ABC and △ADC are isosceles triangles and BD bisects ∠ABC and ∠ADC, applying the Exterior Angle Theorem to △ABD gives ∠BAD=70∘− 20∘=(D)50∘.
The problems on this page are the property of the MAA's American Mathematics Competitions