Problem:
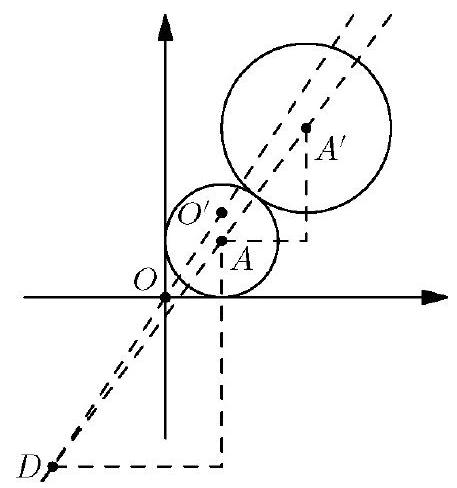
A dilation of the plane-that is, a size transformation with a positive scale factor-sends the circle of radius centered at to the circle of radius centered at . What distance does the origin move under this transformation?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The scale factor for this transformation is . The center of the dilation, , must lie along ray (with between and ), and its distance from must be of its distance from . Because is units to the left of and units below , the center of the dilation must be 6 units to the left of and units below , placing it at . The origin is units from , so the dilation must move it half that far, or units. Alternatively, note that the origin is units to the right of and units above , so its image must be units to the right of and units above ; therefore it is located at , a distance from the origin.
The problems on this page are the property of the MAA's American Mathematics Competitions