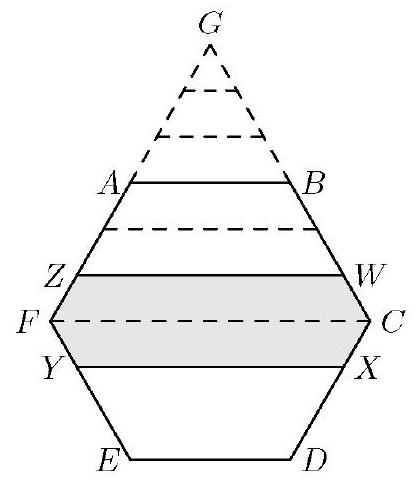
Problem:
In regular hexagon ABCDEF, points W,X,Y, and Z are chosen on sides BC, CD,EF, and FA, respectively, so that lines AB,ZW,YX, and ED are parallel and equally spaced. What is the ratio of the area of hexagon WCXYFZ to the area of hexagon ABCDEF?
Answer Choices:
A. 31
B. 2710
C. 2711
D. 94
E. 2713
Solution:
Extend sides CB and FA to meet at G. Note that FC=2AB and ZW=35AB. Then the areas of △BAG,△WZG, and △CFG are in the ratio 12:(35)2:22=9:25:36. Thus ∣ABCF][ZWCF]=36−936−25=2711, and by symmetry, [ABCDEF][WCXYFZ]=(C)2711 also.
OR
Suppose that AB=1; then FZ=31 and FC=2. Trapezoid WCFZ, which is the upper half of hexagon WCXYFZ, can be tiled by 11 equilateral triangles of side length 31, and the lower half similarly, making 22 such triangles. Hexagon ABCDEF can be tiled by 6 equilateral triangles of side length 1, and each of these can be tiled by 9 equilateral triangles of side length 31, making a total of 6⋅9=54 small triangles. The required ratio is 5422=(C)2711.
The problems on this page are the property of the MAA's American Mathematics Competitions