Problem:
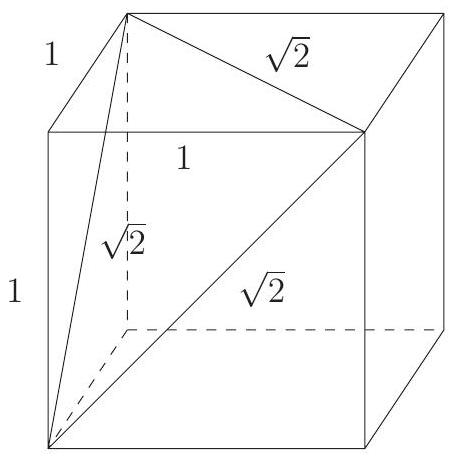
A solid tetrahedron is sliced off a solid wooden unit cube by a plane passing through two nonadjacent vertices on one face and one vertex on the opposite face not adjacent to either of the first two vertices. The tetrahedron is discarded and the remaining portion of the cube is placed on a table with the cut surface face down. What is the height of this object?
Answer Choices:
A.
B.
C.
D.
E. \sqrt
Solution:
The discarded tetrahedron can be viewed as having an isosceles right triangle of side as its base, with an altitude of . Therefore its volume is . It can also be viewed as having an equilateral triangle of side length as its base, in which case its altitude must satisfy
which implies that . The height of the remaining solid is the long diagonal of the cube minus , which is .
The problems on this page are the property of the MAA's American Mathematics Competitions