Problem:
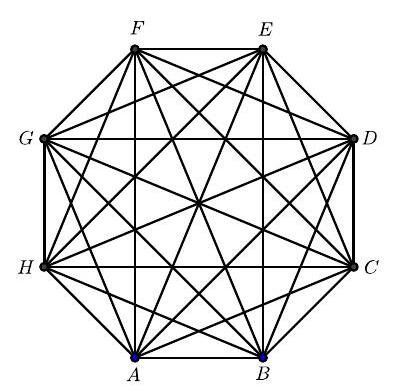
All diagonals are drawn in a regular octagon. At how many distinct points in the interior of the octagon (not on the boundary) do two or more diagonals intersect?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Label the octagon . There are diagonals in all, with endpoints at each vertex. The diagonals are of three types:
Diagonals that skip over only one vertex, such as or . These diagonals intersect with each of the five diagonals with endpoints at the skipped vertex.
Diagonals that skip two vertices, such as or . These diagonals intersect with four of the five diagonals that have endpoints at each of the two skipped vertices.
Diagonals that cross to the opposite vertex, such as . These diagonals intersect with three of the five diagonals that have endpoints at each of the three skipped vertices.
Therefore, from any given vertex, the diagonals will intersect other diagonals at points. Counting from all vertices, the total is points.
Observe that, by symmetry, all four diagonals that cross to the opposite vertex intersect in the center of the octagon. This single intersection point has been counted times, from each of the vertices. Further observe that at each of the vertices of the smallest internal octagon created by the diagonals, diagonals intersect. For example, intersects with on . These intersection points have each been counted times, from each of the affected vertices. The remaining intersection points each involve only two diagonals and each has been counted times, once from each endpoint. These number . There are therefore distinct intersection points in the interior of the octagon.
The problems on this page are the property of the MAA's American Mathematics Competitions