Problem:
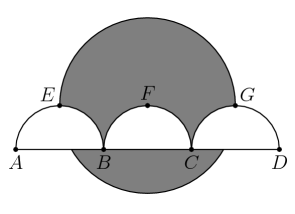
As shown in the figure, line segment is trisected by points and so that . Three semicircles of radius , , and , have their diameters on , lie in the same halfplane determined by line , and are tangent to line at , , and , respectively. A circle of radius has its center at . The area of the region inside the circle but outside the three semicircles, shaded in the figure, can be expressed in the form
where , and are positive integers and and are relatively prime. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let and be the intersections of with the circle centered at , where lies between and , and lies between and ; and let be the foot of the perpendicular line segment from to . The specified region consists of three subregions: a semicircle of radius , a rectangle with quarter circles of radius removed, and the segment of the circle cut off by chord , as shown in the figure below.
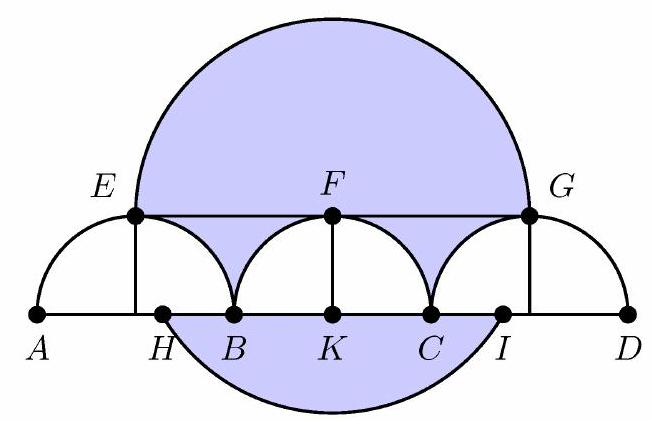
The semicircle of radius has area . The rectangle minus the quarter circles has area . Because and , it follows that has measure , and therefore the segment of the circle is a third of the circle with removed. The area of the segment is
Adding the areas of the three subregions gives , and the requested sum is .
The problems on this page are the property of the MAA's American Mathematics Competitions