Problem:
The figure below shows circles of radius within a larger circle. All the intersections occur at points of tangency. What is the area of the region, shaded in the figure, inside the larger circle but outside all of the circles of radius ?
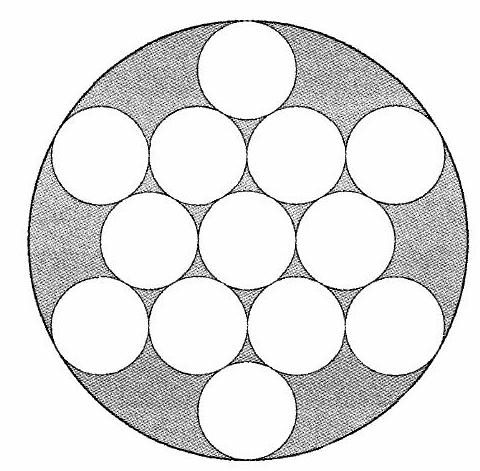
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let , and be the centers of four of the circles as shown below, and let be the intersection of the diagonals of rhombus . Then and , so ; similarly . The radius of the large circle is therefore . The requested area is
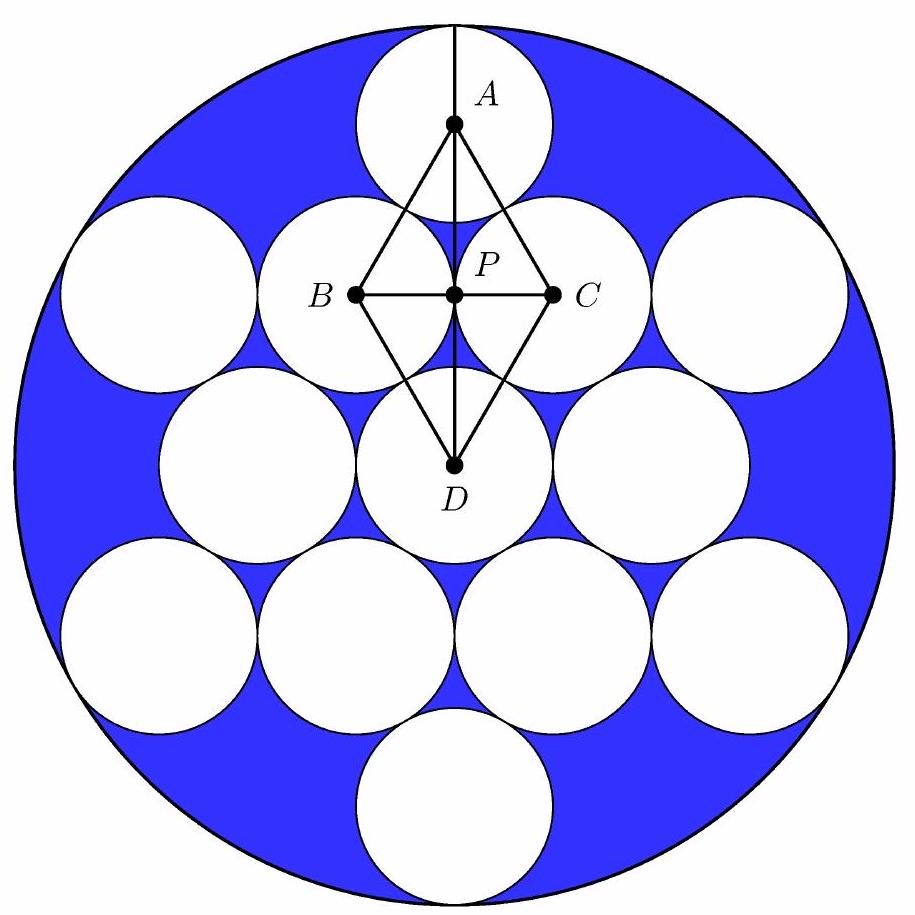
Note: This problem is related to the question of how densely the plane can be packed with congruent circles - how much wasted space there is with the most efficient packing. It has been proved that the best arrangement is the one shown in this problem, with each circle surrounded by six others. The fraction of the plane covered by the circles is .
The problems on this page are the property of the MAA's American Mathematics Competitions