Problem:
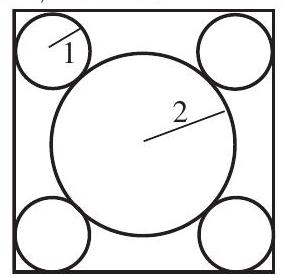
Four circles of radius are each tangent to two sides of a square and externally tangent to a circle of radius , as shown. What is the area of the square?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let be the length of a side of the square. Consider an isosceles right triangle with vertices at the centers of the circle of radius and two of the circles of radius . This triangle has legs of length , so its hypotenuse has length .
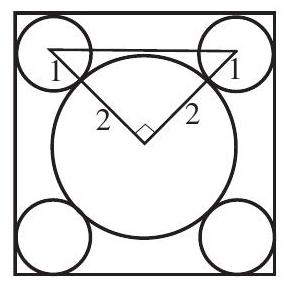
The length of a side of the square is more than the length of this hypotenuse, so . Hence the area of the square is
The distance from a vertex of the square to the center of the nearest small circle is , and the distance between the centers of two small circles in opposite corners of the square is . Therefore each diagonal of the square has length , and each side has length
The area of the square is consequently .
The problems on this page are the property of the MAA's American Mathematics Competitions