Problem:
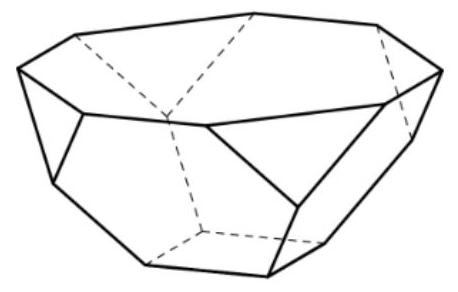
A bowl is formed by attaching four regular hexagons of side to a square of side . The edges of the adjacent hexagons coincide, as shown in the figure. What is the area of the octagon obtained by joining the top eight vertices of the four hexagons, situated on the rim of the bowl?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Adjacent hexagons with side length 1 are folded up so that a square with side length 1 -the base of the bowl-exactly fits in the gap between them. By symmetry, a square of side length 1 must also fit in the other gap formed by those two hexagons. It follows that the distance between the closest vertices on adjacent hexagons on the top of the bowl are units apart - the diagonal of a unit square. Therefore the required octagon is as shown below.
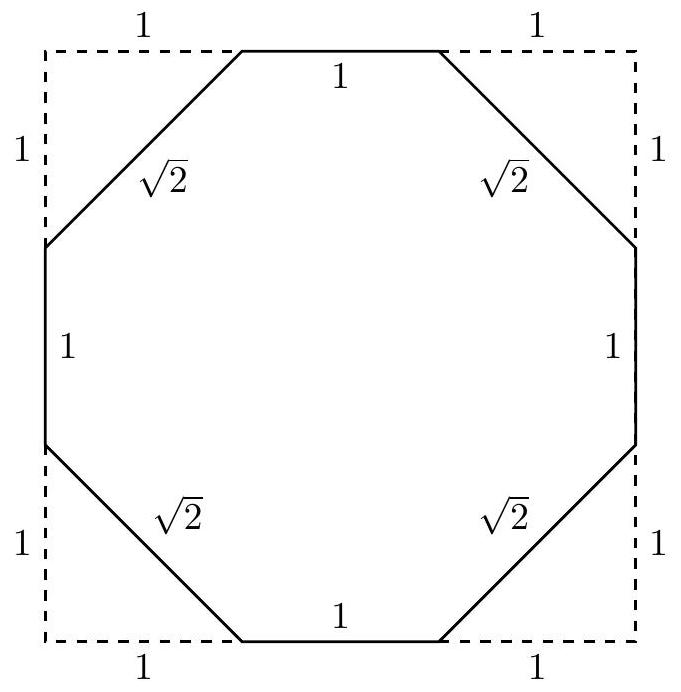
Its area is the area of the square minus the areas of the four isosceles right triangular corners, namely
The problems on this page are the property of the MAA's American Mathematics Competitions