Problem:
Two circles of radius are externally tangent to each other and are internally tangent to a circle of radius at points and , as shown in the diagram. The distance can be written in the form , where and are relatively prime positive integers. What is ?
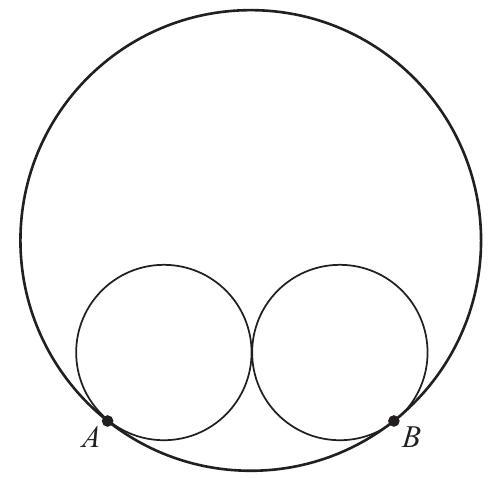
Answer Choices:
A.
B.
C.
D.
E.
Solution:
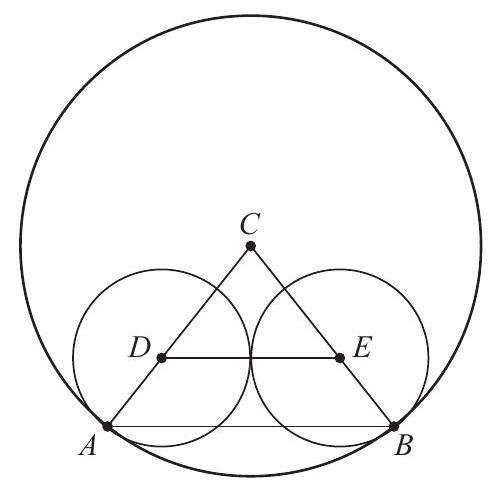
Let be the center of the larger circle, and let and be the centers of the two smaller circles, as shown. Points , and are collinear because the radii are perpendicular to the common tangent at the point of tangency, and so are , and . These points form two isosceles triangles that share a vertex angle. Thus , and therefore , so
and the requested sum is .
The problems on this page are the property of the MAA's American Mathematics Competitions