Problem:
Jacob uses the following procedure to write down a sequence of numbers. First he chooses the first term to be . To generate each succeeding term, he flips a fair coin. If it comes up heads, he doubles the previous term and subtracts . If it comes up tails, he takes half of the previous term and subtracts . What is the probability that the fourth term in Jacob's sequence is an integer?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The tree diagram below gives all possible sequences of four terms. In the diagram, each left branch from a number corresponds to a head, and each right branch to a tail.
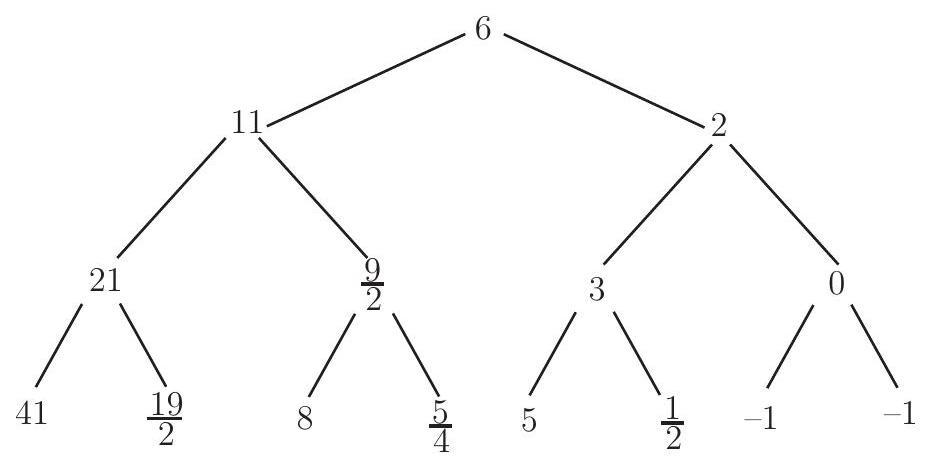
Because the coin is fair, each of the eight possible outcomes in the bottom row of the diagram is equally likely. Five of those numbers are integers, so the required probability is .
The problems on this page are the property of the MAA's American Mathematics Competitions