Problem:
The faces of each of standard dice are labeled with the integers from to . Let be the probability that when all dice are rolled, the sum of the numbers on the top faces is . What other sum occurs with the same probability ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
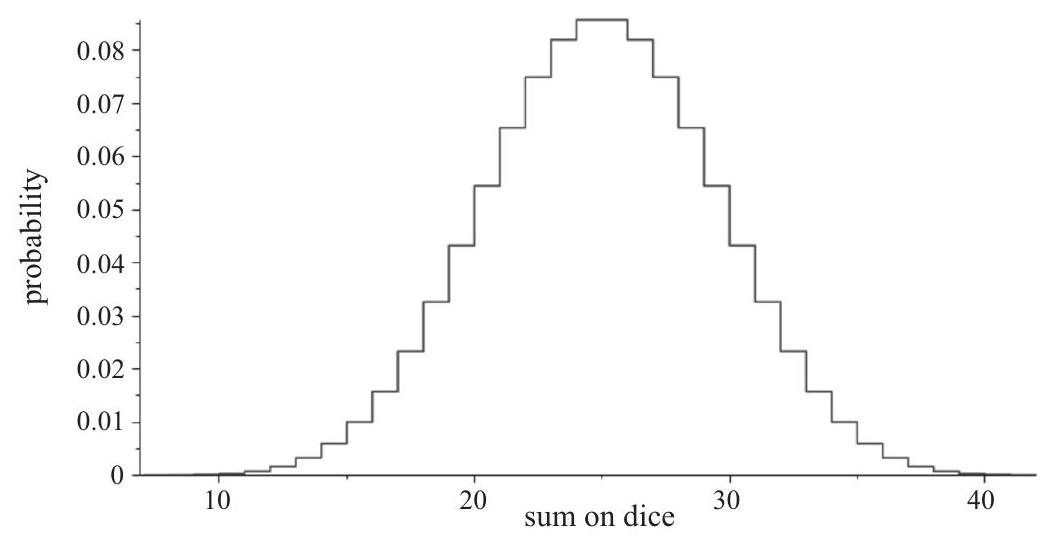
Without loss of generality, one can assume that the numbers on opposite faces of each die add up to . In other words, the is opposite the , the is opposite the , and the is opposite the . (In fact, standard dice are numbered in this way.) The top faces give a sum of if and only if the bottom faces give a sum of . By symmetry, the probability that the top faces give a sum of is also . The distribution of the outcomes of the dice rolls has the bell-shaped graph shown below, so no other outcome has the same probability as and .
The problems on this page are the property of the MAA's American Mathematics Competitions