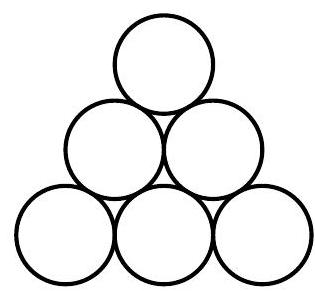
Problem:
In the figure below, of the disks are to be painted blue, are to be painted red, and is to be painted green. Two paintings that can be obtained from one another by a rotation or a reflection of the entire figure are considered the same. How many different paintings are possible?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
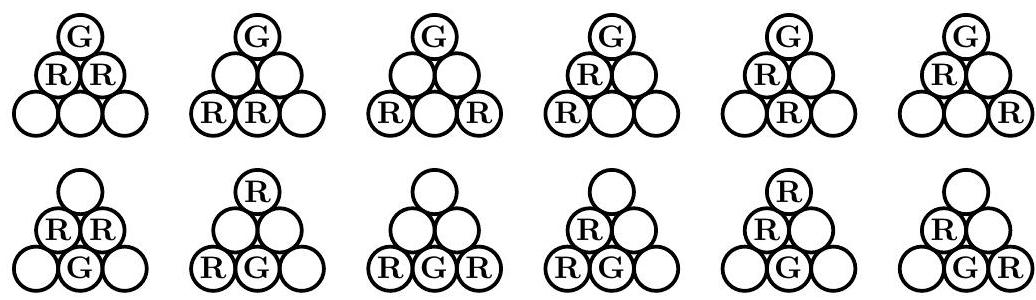
By symmetry, there are just two cases for the position of the green disk: corner or non-corner. If a corner disk is painted green, then there is case in which both red disks are adjacent to the green disk, there are cases in which neither red disk is adjacent to the green disk, and there are cases in which exactly one of the red disks is adjacent to the green disk. Similarly, if a non-corner disk is painted green, then there is case in which neither red disk is in a corner, there are cases in which both red disks are in a corner, and there are cases in which exactly one of the red disks is in a corner. The total number of paintings is .
The problems on this page are the property of the MAA's American Mathematics Competitions