Problem:
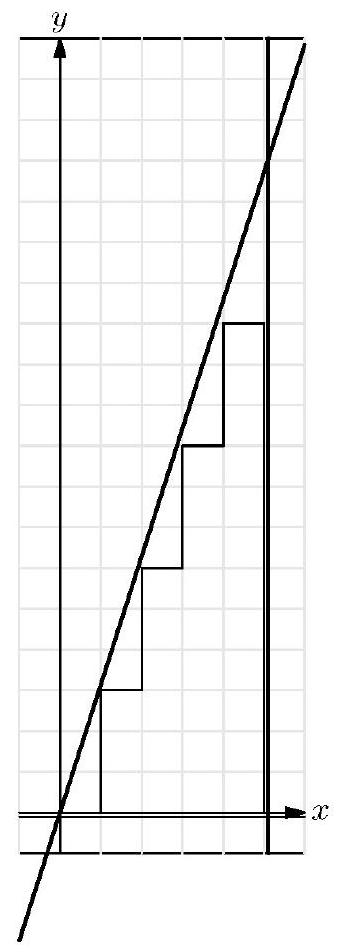
How many squares whose sides are parallel to the axes and whose vertices have coordinates that are integers lie entirely within the region bounded by the line , the line , and the line ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Note that , and . Therefore there are -by- squares of the desired type in the strip -by- squares in the strip -by- squares in the strip , and -by- squares in the strip . Furthermore there are -by- squares in the strip -by- squares in the strip , and -by- squares in the strip . There is -by- square in the strip , and there are -by- squares in the strip . There are no -by- or larger squares. Thus in all there are squares of the desired type within the given region.
The problems on this page are the property of the MAA's American Mathematics Competitions