Problem:
A bug travels from to along the segments in the hexagonal lattice pictured below. The segments marked with an arrow can be traveled only in the direction of the arrow, and the bug never travels the same segment more than once. How many different paths are there?
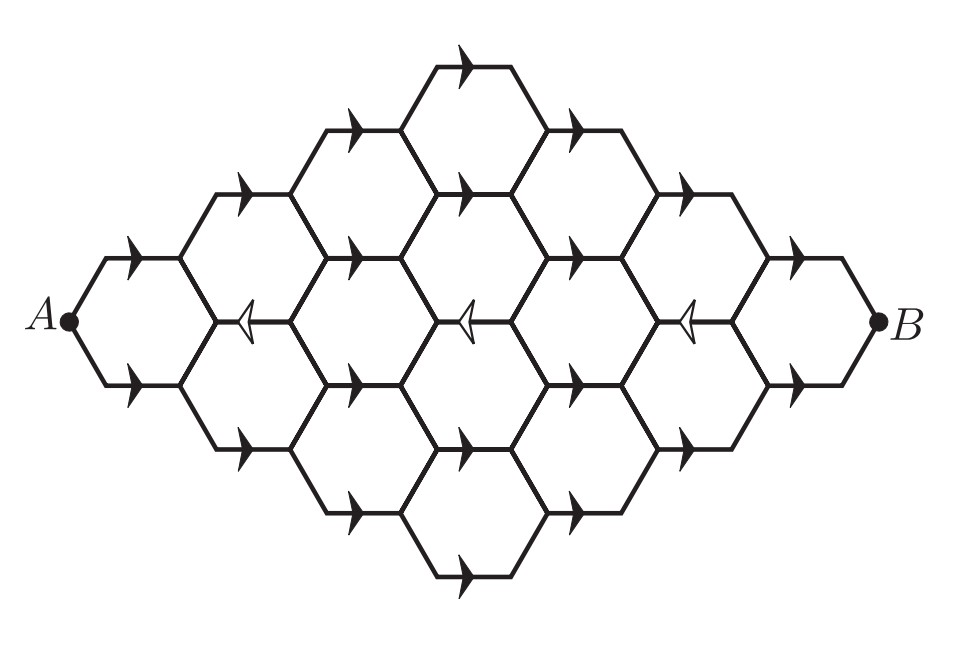
Answer Choices:
A.
B.
C.
D.
E.
Solution:
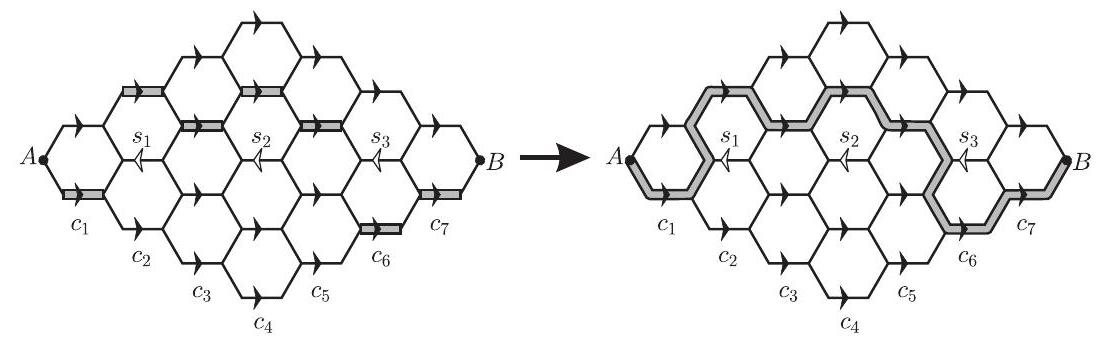
Label the columns having arrows as according to the figure. Call those segments that can be traveled only from left to right forward segments. Call the segments , and , in columns , and , respectively, which can be traveled only from right to left, back segments. Denote as the set of back segments traveled for a path.
First suppose that . Because it is not possible to travel a segment more than once, it follows that the path is uniquely determined by choosing one forward segment in each of the columns . There are , and choices for the forward segment in columns , and , respectively. This gives a total of total paths in this case.
Next suppose that . The two forward segments in , together with , need to be part of the path, and once the forward segment from is chosen, the order in which the segments of are traveled is determined. Moreover, there are only choices for possible segments in depending on the last segment traveled in , either the bottom or the top . For the rest of the columns, the path is determined by choosing any forward segment. Thus the total number of paths in this case is , and by symmetry this is also the total for the number of paths when . A similar argument gives trips for the case when .
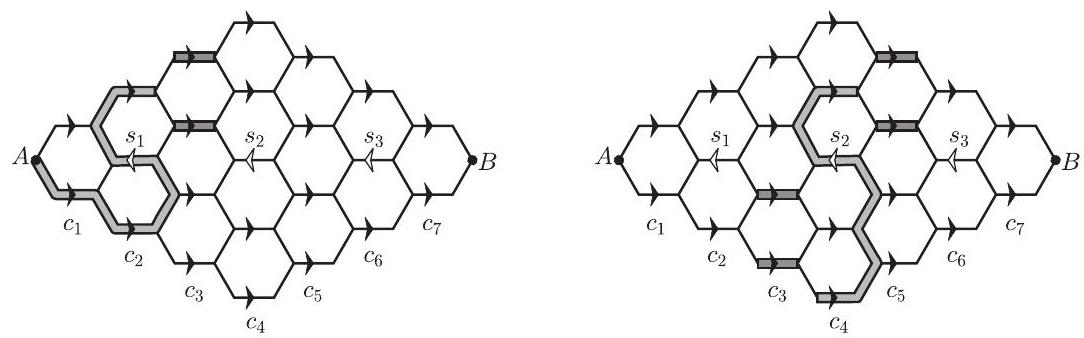
Suppose . Because is traveled, it follows that forward segments in need to belong to the path, one of them above ( choices) and the other below it ( choices). Once these are determined, there are possible choices for the order in which these segments are traveled: the bottom forward segment first, then , then the top forward segment, or vice versa. Next, there are only possible forward segments that can be selected in and also only possible forward segments that can be selected in . The forward segments in , and can be freely selected ( choices each). This gives a total of paths.
If , then the analysis is similar, except for the last step, where the forward segments of and are determined by the previous choices. Thus there are possibilities, and by symmetry the same number when .
Finally, if , then in the last step, all forward segments of , and are determined by the previous choices and hence there are possible paths. Altogether the total number of paths is .
The problems on this page are the property of the MAA's American Mathematics Competitions