Problem:
All the numbers are written in a array of squares, one number in each square, in such a way that if two numbers are consecutive then they occupy squares that share an edge. The numbers in the four corners add up to . What number is in the center?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
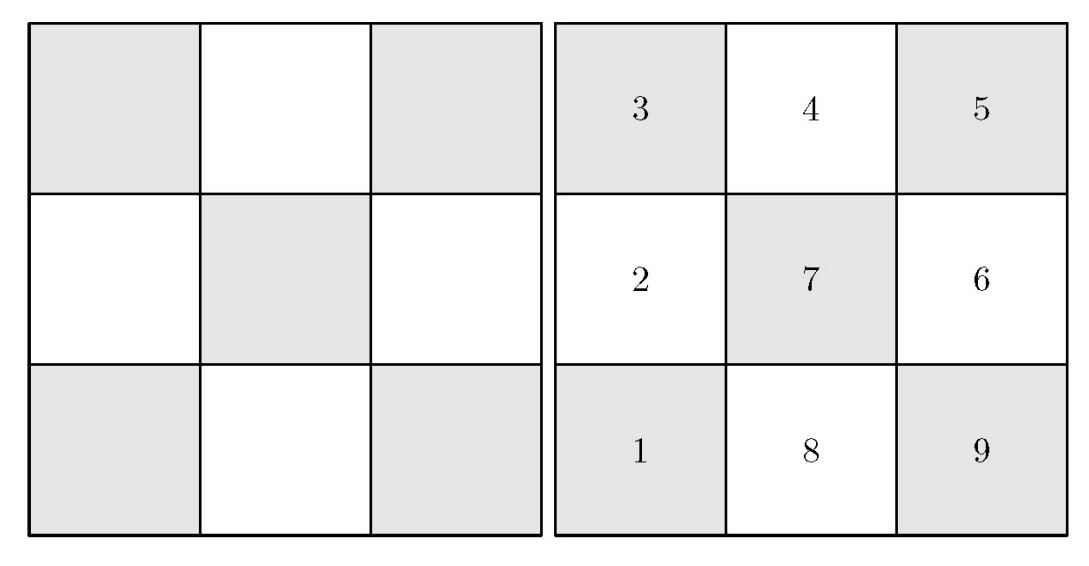
Shade the squares in a checkerboard pattern as shown in the first figure. Because consecutive numbers must be in adjacent squares, the shaded squares will contain either five odd numbers or five even numbers. Because there are only four even numbers available, the shaded squares contain the five odd numbers. Thus the sum of the numbers in all five shaded squares is . Because all but the center add up to , the center number must be . The situation described is actually possible, as the second figure demonstrates.
The problems on this page are the property of the MAA's American Mathematics Competitions