Problem:
In the figure below, 3 of the 6 disks are to be painted blue, 2 are to be painted red, and 1 is to be painted green. Two paintings that can be obtained from one another by a rotation or a reflection of the entire figure are considered the same. How many different paintings are possible?
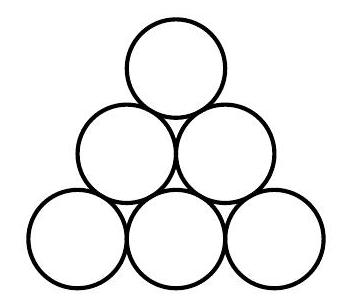
Answer Choices:
A.
B.
C.
D.
E.
Solution:
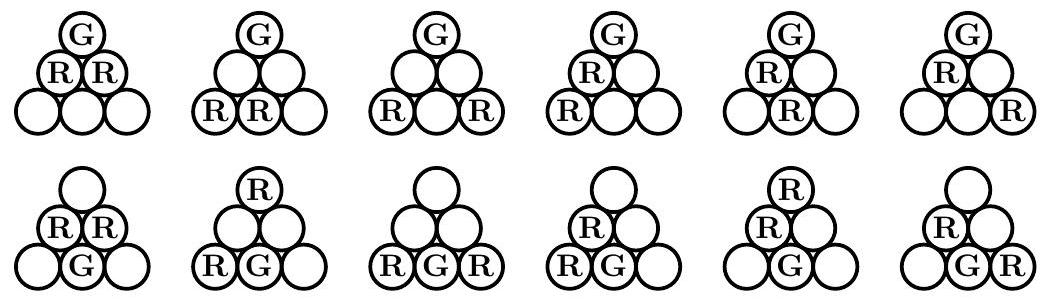
By symmetry, there are just two cases for the position of the green disk: corner or non-corner. If a corner disk is painted green, then there is 1 case in which both red disks are adjacent to the green disk, there are 2 cases in which neither red disk is adjacent to the green disk, and there are 3 cases in which exactly one of the red disks is adjacent to the green disk. Similarly, if a non-corner disk is painted green, then there is 1 case in which neither red disk is in a corner, there are 2 cases in which both red disks are in a corner, and there are 3 cases in which exactly one of the red disks is in a corner. The total number of paintings is .
The problems on this page are the property of the MAA's American Mathematics Competitions