Problem:
Let be an equiangular convex pentagon of perimeter 1 . The pairwise intersections of the lines that extend the sides of the pentagon determine a fivepointed star polygon. Let be the perimeter of this star. What is the difference between the maximum and the minimum possible values of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
The sum of the internal angles of the pentagon is and by assumption all internal angles are equal, so they are all equal to . Therefore the supplementary angles at each of the vertices are all equal to . It follows that all the triangles making up the points of the star are isosceles triangles with angles measuring , and . Label the rest of the vertices of the star as in the figure. By the above argument, there is a constant such that and similar expressions for the other four points of the star. Therefore the required perimeter equals
and therefore the maximum and minimum values are the same and their difference is .
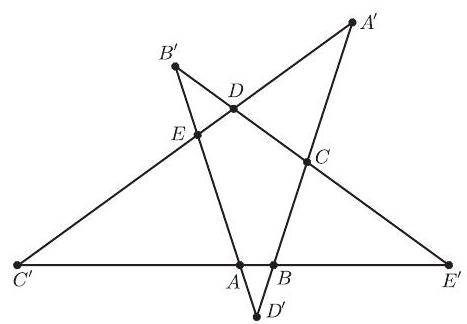
Note: The constant equals .
The problems on this page are the property of the MAA's American Mathematics Competitions