Problem:
A sphere is inscribed in a truncated right circular cone as shown. The volume of the truncated cone is twice that of the sphere. What is the ratio of the radius of the bottom base of the truncated cone to the radius of the top base of the truncated cone?

Answer Choices:
A.
B.
C.
D.
E.
Solution:
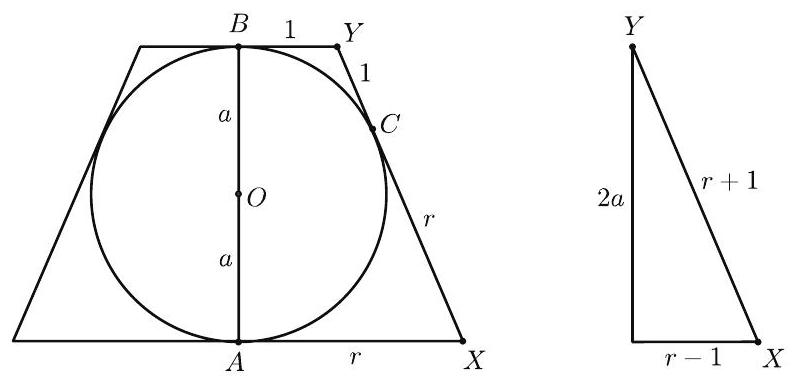
Assume without loss of generality that the radius of the top base of the truncated cone (frustum) is 1 . Denote the radius of the bottom base by and the radius of the sphere by . The figure on the left is a side view of the frustum. Applying the Pythagorean Theorem to the triangle on the right yields . The volume of the frustum is
Setting this equal to twice the volume of the sphere, , and simplifying gives , or . Therefore .
The problems on this page are the property of the MAA's American Mathematics Competitions