Problem:
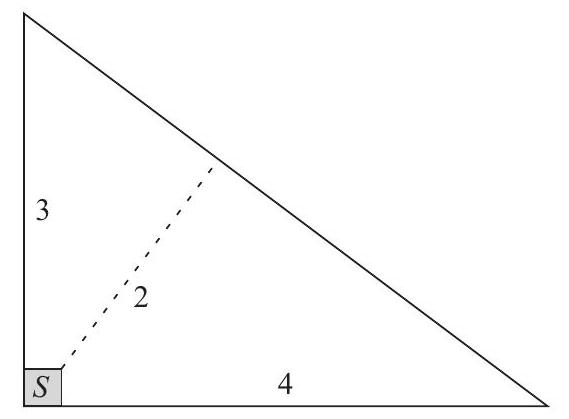
Farmer Pythagoras has a field in the shape of a right triangle. The right triangle's legs have lengths of and units. In the corner where those sides meet at a right angle, he leaves a small unplanted square so that from the air it looks like the right angle symbol. The rest of the field is planted. The shortest distance from to the hypotenuse is units. What fraction of the field is planted?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let the triangle's vertices in the coordinate plane be , and , with representing the unplanted portion of the field. The equation of the hypotenuse is , so the distance from , the corner of closest to the hypotenuse, to this line is given by
Setting this equal to 2 and solving for gives and , and the former is rejected because the square must lie within the triangle. The unplanted area is thus , and the requested fraction is
OR
Let the given triangle be described as with the right angle at and . Let be the vertex of the square that is in the interior of the triangle, and let be the edge length of the square. Then two sides of the square along with line segments and decompose into four regions. These regions are a triangle with base 5 and height 2 , the unplanted square with side , a right triangle with legs and , and a right triangle with legs and . The sum of the areas of these four regions is
and the area of is . Solving for gives , and the solution concludes as above.
The problems on this page are the property of the MAA's American Mathematics Competitions