Problem:
A plane contains points and with . Let be the union of all disks of radius 1 in the plane that cover . What is the area of ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
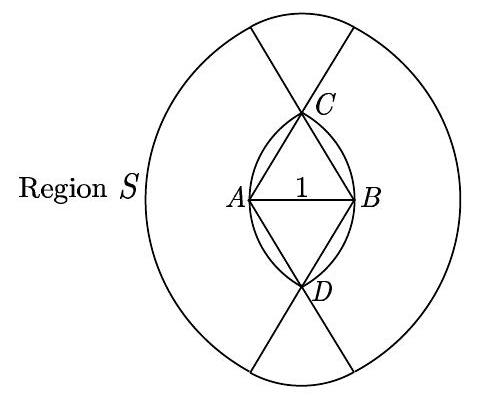
The center of the disk lies in a region , consisting of all points within 1 unit of both and . Let and be the points of intersection of the circles of radius 1 centered at and . Because and are equilateral, and are each 120 . Thus the sector bounded by , and has area , as does the sector bounded by , and arc . The intersection of the two sectors, which is the union of the two triangles, has area , so the area of is
.jpg)
The region consists of all points within 1 unit of . In addition to itself, contains two 60 sectors of radius 1 and two 120 annuli of outer radius 2 and inner radius 1. The area of each sector is , and the area of each annulus is
Therefore the area of is
The problems on this page are the property of the MAA's American Mathematics Competitions