Problem:
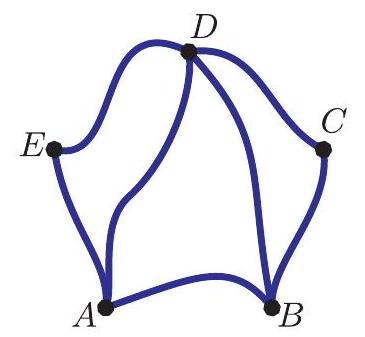
Cities , and are connected by roads , and . How many different routes are there from to that use each road exactly once? (Such a route will necessarily visit some cities more than once.)
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Cities and and the roads leading in and out of them can be replaced by a second road and a second road, respectively. If routes are designated by the list of cities they visit in order, then there are 4 types of routes: , and . Each type of route represents 4 actual routes, because the trip between and can include the detour through either the first or the second time, and a similar choice applies for the trip between and . Therefore there are different routes.
The problems on this page are the property of the MAA's American Mathematics Competitions