Problem:
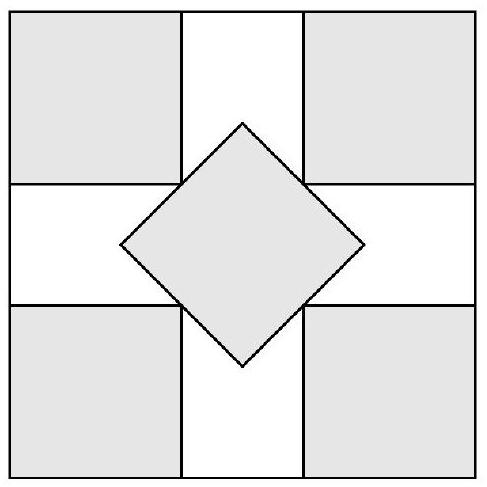
The five small shaded squares inside this unit square are congruent and have disjoint interiors. The midpoint of each side of the middle square coincides with one of the vertices of the other four small squares as shown. The common side length is , where and are positive integers. What is
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let be the common side length. Draw a diagonal between opposite corners of the unit square. The length of this diagonal is . The diagonal consists of two small-square diagonals and one small-square side length. Combining the previous two observations yields
Solving this equation for gives . The requested sum is .
OR
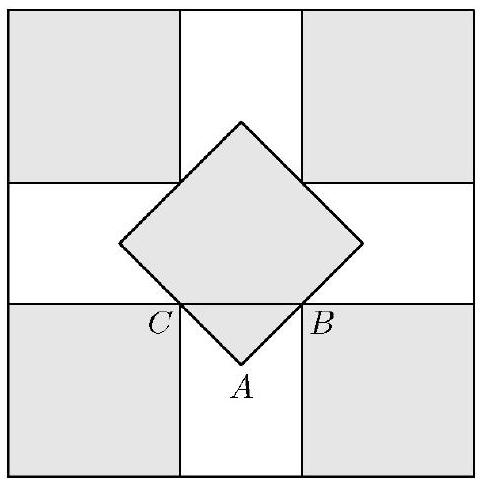
Again let be the common side length. Triangle in the figure shown is a right triangle with sides , and . By the Pythagorean Theorem,
Solving this equation and noting that yields , as above.
The problems on this page are the property of the MAA's American Mathematics Competitions