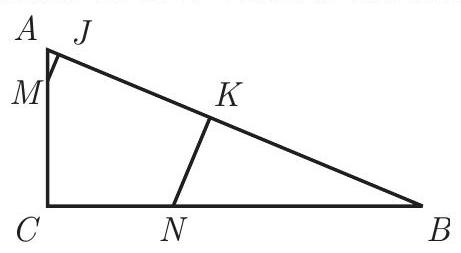
Problem:
In â–³ABC,AB=13,AC=5 and BC=12. Points M and N lie on AC and BC, respectively, with CM=CN=4. Points J and K are on AB so that MJ and NK are perpendicular to AB. What is the area of pentagon CMJKN ?
Answer Choices:
A. 15
B. 581​
C. 12205​
D. 13240​
E. 20
Solution:
Because â–³ABC,â–³NBK, and â–³AMJ are similar right triangles whose hypotenuses are in the ratio 13:8:1, their areas are in the ratio 169:64:1.
The area of △ABC is 21​(12)(5)=30, so the areas of △NBK and △AMJ are 16964​(30) and 1691​(30), respectively.
Thus the area of pentagon CMJKN is (1−16964​−1691​)(30)=240/13​.
The problems on this page are the property of the MAA's American Mathematics Competitions
