Problem:
Let and be points in the plane. Define as the region in the first quadrant consisting of those points such that is an acute triangle. What is the closest integer to the area of the region ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
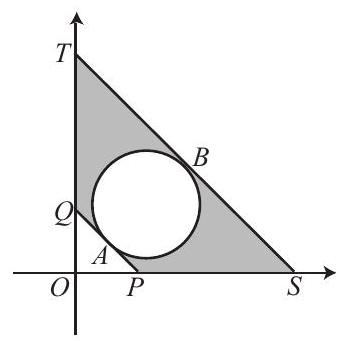
For to be acute, all angles must be acute. For to be acute, point must lie above the line passing through and perpendicular to . The segment of that line in the first quadrant lies between and . For to be acute, point must lie below the line through and perpendicular to . The segment of that line in the first quadrant lies between and . For to be acute, point must lie outside the circle that has as a diameter. Let denote the origin. Region , shaded below, has area equal to
Area Circle
The problems on this page are the property of the MAA's American Mathematics Competitions