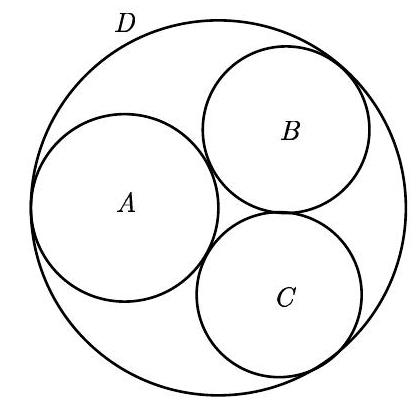
Problem:
Circles , and are externally tangent to each other and internally tangent to circle . Circles and are congruent. Circle has radius 1 and passes through the center of . What is the radius of circle ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let , and be the centers of circles , and , respectively, and let be the point of tangency of circles and . Let and . Since the center of circle lies on circle and the circles have a common point of tangency, the radius of circle is 2 , which is the diameter of circle . Applying the Pythagorean Theorem to right triangles EGH and gives
from which it follows that
The solutions of this system are and . The radius of circle is the positive solution for , which is .

The problems on this page are the property of the MAA's American Mathematics Competitions