Problem:
Let be a square of side length 1 . Two points are chosen independently at random on the sides of . The probability that the straight-line distance between the points is at least is , where , and are positive integers and . What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let the square have vertices , and , and consider three cases.
Case 1: The chosen points are on opposite sides of the square. In this case the distance between the points is at least with probability 1 .
Case 2: The chosen points are on the same side of the square. It may be assumed that the points are and . The pairs of points in the -plane that meet the requirement are those within the square that satisfy either or . These inequalities describe the union of two isosceles right triangles with leg length , together with their interiors. The area of the region is , and the area of the square is 1 , so the probability that the pair of points meets the requirement in this case is .
Case 3: The chosen points are on adjacent sides of the square. It may be assumed that the points are and . The pairs of points in the -plane that meet the requirement are those within the square that satisfy . These inequalities describe the region inside the square and outside a quarter-circle of radius . The area of this region is , which is also the probability that the pair of points meets the requirement in this case.
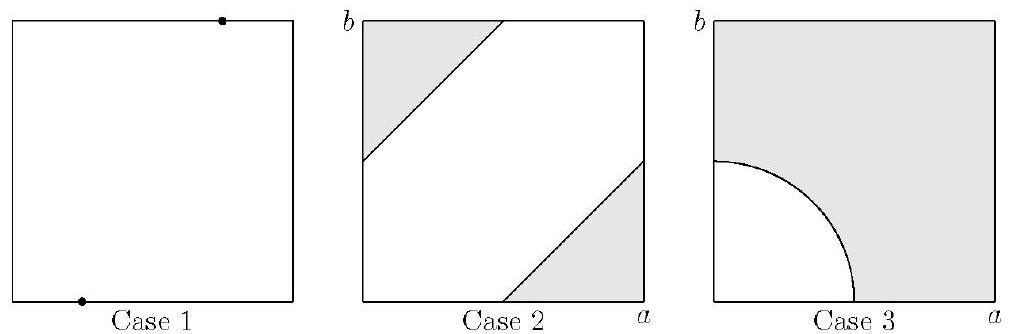
Cases 1 and 2 each occur with probability , and Case 3 occurs with probability . The requested probability is
and .
The problems on this page are the property of the MAA's American Mathematics Competitions