Problem:
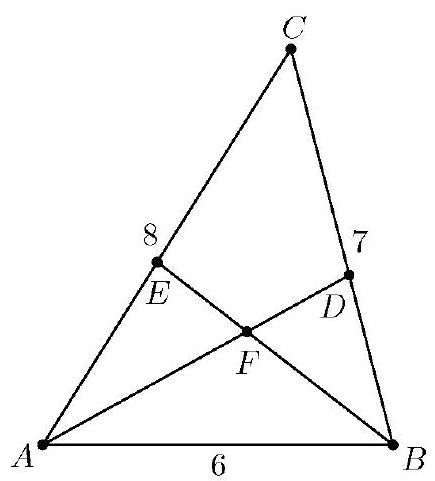
In △ABC,AB=6,BC=7, and CA=8. Point D lies on BC, and AD bisects ∠BAC. Point E lies on AC, and BE bisects ∠ABC. The bisectors intersect at F. What is the ratio AF:FD?
Answer Choices:
A. 3:2
B. 5:3
C. 2:1
D. 7:3
E. 5:2
Solution:
Applying the Angle Bisector Theorem to △BAC gives BD : DC=6:8, so BD=6+86⋅7=3. Then applying the Angle Bisector Theorem to △ABD gives AF:FD=6:3=2:1.
Note: More generally the ratio AF:FD is (AB+CA):BC, which equals 2:1 whenever AB,BC,CA forms an arithmetic progression.
The problems on this page are the property of the MAA's American Mathematics Competitions