Problem:
For each x in [0,1], define
f(x)=⎩⎪⎪⎨⎪⎪⎧2x, if 0≤x≤212−2x, if 21<x≤1
Let f[2](x)=f(f(x)), and f[n+1](x)=f[n](f(x)) for each integer n≥2. For how many values of x in [0,1] is f[2005](x)=1/2?
Answer Choices:
A. 0
B. 2005
C. 4010
D. 20052
E. 22005
Solution:
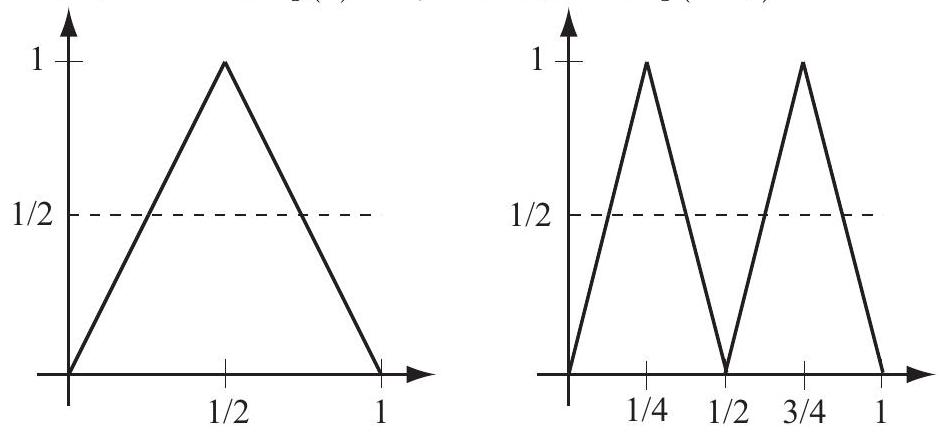
The graphs of y=f(x) and y=f[2](x) are shown below. For n≥2 we have
f[n](x)=f[n−1](f(x))=⎩⎪⎪⎨⎪⎪⎧f[n−1](2x), if 0≤x≤21f[n−1](2−2x), if 21≤x≤1
Let g(n) be the number of values of x in [0,1] for which f[n](x)=1/2. Then f[n](x)=1/2 for g(n−1) values of x in [0,1/2] and g(n−1) values of x in [1/2,1]. Furthermore f[n](1/2)=f[n−1](1)=0=1/2 for n≥2. Hence g(n)=2g(n−1) for each n≥2. Because g(1)=2, it follows that g(2005)=22005.
The problems on this page are the property of the MAA's American Mathematics Competitions