Problem:
Four regular hexagons surround a square with a side length , each one sharing an edge with the square, as shown in the figure below. The area of the resulting -sided outer nonconvex polygon can be written as , where , and are integers and is not divisible by the square of any prime. What is ?
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Let be the upper-right corner of the original unit square, and let , and be the three consecutive vertices of the outer 12 -sided polygon that are closest to , as shown below. Lines and meet at , and lines and meet at . Let be the foot of the perpendicular from to .
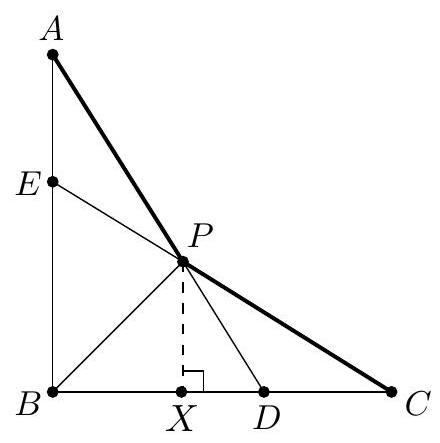
Note that is contained in a diagonal of the rightmost hexagon. Because each hexagon has side length 1 , this diagonal has length . As a result, . Set . Triangle is a triangle, so . Triangle is a triangle, so . Thus
so
The area of concave quadrilateral is twice the area of . It follows that the area of the quadrilateral is
Finally, observe that the original figure decomposes into four copies of concave quadrilateral , four rectangles of dimensions , and one unit square. It follows that the total area of the figure is
The requested sum is .
The problems on this page are the property of the MAA's American Mathematics Competitions