Problem:
The graph below shows a portion of the curve defined by the quartic polynomial . Which of the following is the smallest?
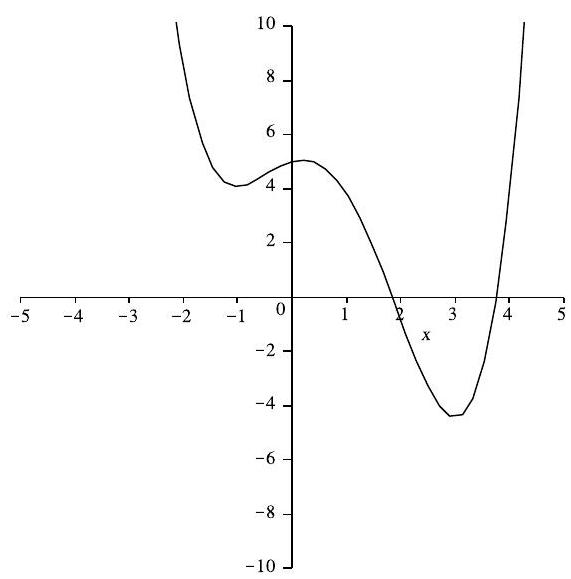
Answer Choices:
A.
B. $The product of the zeros of $
C. $The product of the non-real zeros of $
D. $The sum of the coefficients of $
E. $The sum of the real zeros of $
Solution:
First note that the quartic polynomial can have no more real zeros than the two shown. (If it did, the quartic would have more than four zeros.) The sum of the coefficients of is , which is greater than 3 . The product of all zeros of is the constant term of the polynomial, which is the -intercept, which is greater than 5 . The sum of the real zeros of (the sum of the -intercepts) is greater than 4.5 , and is greater than 4 . However, since the product of the real zeros of is greater than 4.5 and the product of all the zeros is less than 6 , it follows that the product of all the zeros is less than 6 , it follows that the product of the non-real zeros of is less than 2 , making it the smallest of the numbers.
The problems on this page are the property of the MAA's American Mathematics Competitions