Problem:
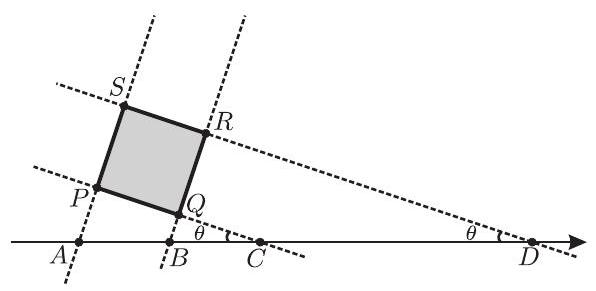
Square PQRS lies in the first quadrant. Points (3,0),(5,0),(7,0), and (13,0) lie on lines SP,RQ,PQ, and SR, respectively. What is the sum of the coordinates of the center of the square PQRS ?
Answer Choices:
A. 6
B. 6.2
C. 6.4
D. 6.6
E. 6.8
Solution:
Let A=(3,0),B=(5,0),C=(7,0),D=(13,0), and θ be the acute angle formed by the line PQ and the x-axis. Then SR=PQ= ABcosθ=2cosθ, and SP=QR=CDsinθ=6sinθ. Because PQRS is a square, it follows that 2cosθ=6sinθ and tanθ=31. Therefore lines SP and RQ have slope 3, and lines SR and PQ have slope −31. Let the points M=(4,0) and N=(10,0) be the respective midpoints of segments AB and CD. Let ℓ1 be the line through M parallel to line SP. Let ℓ2 be the line through N parallel to line SR. Lines ℓ1 and ℓ2 intersect at the center of the square PQRS. Line ℓ1 satisfies the equation y=3(x−4), and line ℓ2 satisfies the equation y=−31(x−10). Thus the lines ℓ1 and ℓ2 intersect at the point (4.6,1.8), and the required sum of coordinates is 6.4 .
The problems on this page are the property of the MAA's American Mathematics Competitions