Problem:
Three circles of radius are drawn in the first quadrant of the -plane. The first circle is tangent to both axes, the second is tangent to the first circle and the -axis, and the third is tangent to the first circle and the -axis. A circle of radius is tangent to both axes and to the second and third circles. What is
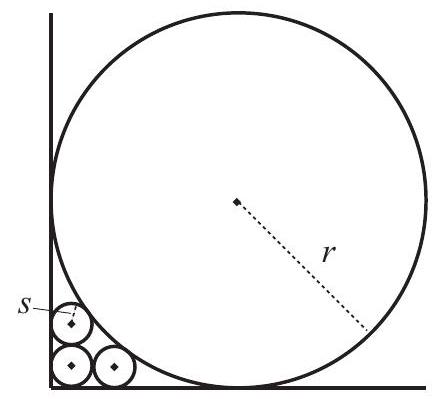
Answer Choices:
A.
B.
C.
D.
E.
Solution:
Consider a right triangle as shown. By the Pythagorean Theorem,
so
and
But , so and .
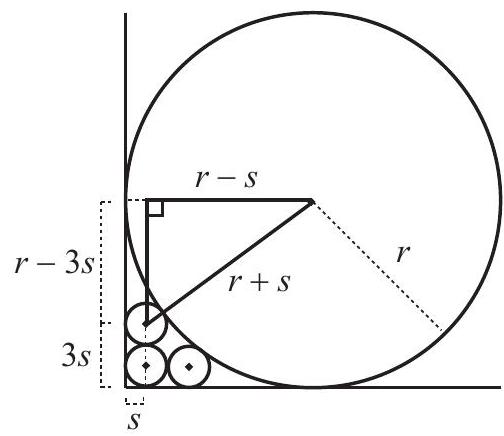
\mathrm
Because the ratio is independent of the value of , assume that and proceed as in the previous solution.
The problems on this page are the property of the MAA's American Mathematics Competitions